L-Garden

-
info : interactive applet
-
date : Jan 2007
-
ware : processing.org
Reaching Complexity
Biological life is complex. It has adapted to nature on many layers and produced good-enough compromises for serving several goals. The need for survival and reproduction seems to demand a system on a very high degree of complexity. A complexity that sometimes doesn't reveal its causal connections to us and is far from anything human-made.
Systems designed by man are usually directed at fulfilling very clear defined tasks. Built in top-down fashion their main advantages are high predictability of behavior and efficiency of operation. Their lack of adaptability though makes them very vulnerable towards changes in their environment.
The field of evolutionary computation borrows the design-process of nature to overcome those disadvantages. Computer programs that mimic the survival of the fittest are able to optimize design solutions in a iterated trial-and-error simulation. Solutions never thought of by man appear out of randomness and recombination. Architecture, robot control or medical prognosis systems have been evolved artificially and show superiority over man-made solutions.
The main critic point against the evolutionary design approach is that it is unable to reach high degrees of complexity. Most examples usually look for solutions in a finite and clearly defined search space. They are bound in the growth of their system to avoid too much randomness and therefore failure. Incremental evolution tries to overcome the bootstrap problem by slowly raising the fitness value and complicating the asked for tasks. But still, the more complex the solution looked for is supposed to be, the fewer successful solutions can be found for direct genotype-phenotype mappings. The same algorithms that work for simple solutions produce too high randomness in larger scales.
Yet complex systems don't consist of completely arbitrary elements. They are structured in a hierarchy of subsystems that work on their own and in connection to other subsystems. Emergent behavior is the product of many simple small units working together. This complexity is reached by designing small functioning entities and then reduplicating them to build larger structures. The L-system eliminates the need for defining systems bit for bit by defining its growing rules instead. Small changes in the rules can cause large effects in the output yet still retain overall functionality. A process similar to the L-system seems to be the effector of growth and form patterns in nature.
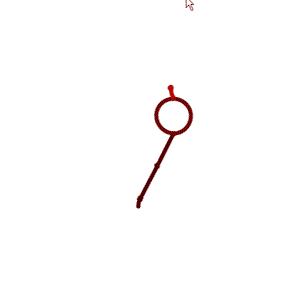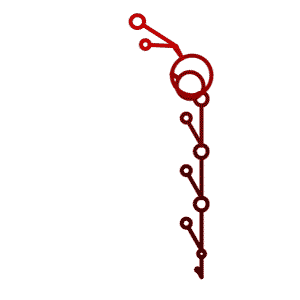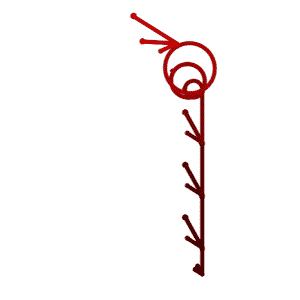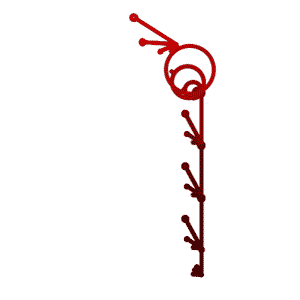
The Program
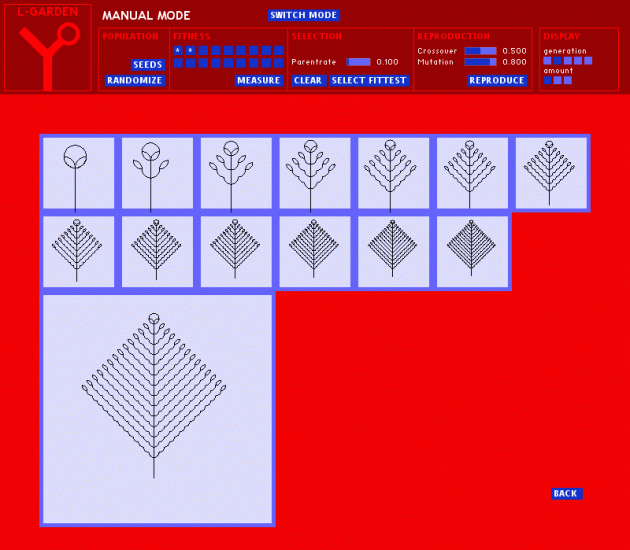
The L-Garden program is a tool for generating and evolving growing rules for drawings through genetic algorithms. The execution of the rules produces commands that lead to abstract drawings. Manual or automatic selection of those drawings leads to the generation of new rules through recombination and mutation.
Each evolutionary run starts typically with a random seed of so-called trees. Each tree consists of a string of symbols defining the initial state, the replacement rule strings for every symbol and a degree value. Symbols in lower case letters were defined not to be replaceable. Each symbol is linked to a task in the final drawing process. The set of available symbols is as follows:
F ... draws a line of step-length
A ... draws an arc of 1 degree-unit clockwise
R ... draws an arc of 1 degree-unit counterclockwise
C ... draws a circle of step-length diameter
J ... without effect
K ... without effect
r ... rotate 1 degree-unit clockwise
b ... rotate 1 degree-unit counterclockwise
j ... jump 1 step-length ahead without drawing
+ ... add one third of the initial step-length to the step-length
- ... subtract one third of the initial step-length from the step-length, but minimize to one third of the initial step-length
By recursively applying the replacement rules in parallel the initial string of symbols is growing the commands for drawing. The population of trees is visualized in their fourth generation. Individuals can be selected by hand to become parents of the next generation. Those trees are transferred into the next generation without alteration. In automatic mode the selection is based on the two values of survival-rate and top-rate. The trees get ranked according to their fitness-value. Those that fall into the top-percentage are defined as parents and are kept without alteration. The rest that still fall into the survival-percentage acts as parents as well, but are not saved. A special algorithm keeps trees with exactly the same rules from being included double into the selection. This prevents the emergence of too many too similar solutions too soon.
The genetic algorithm then perform crossover and mutation operations of growing rules to refill the places of the population that are not inhabited by parents. The crossover algorithm select two parents and the combines their initial string, replacement rules and degree value by breaking the whole set at one random point apart. The mutation algorithm either mutates the initial string, one of the replacement rules or defines a new degree value. When performing string mutations one or several letters can be changed to random symbols, added or subtracted. With a crossover probability of 0.5 and a mutation probability of 0.8 the new generation of trees is built.
The abstract plants and patterns generated by the growing rules can be displayed either by showing generation 1 to 10 next to each other …
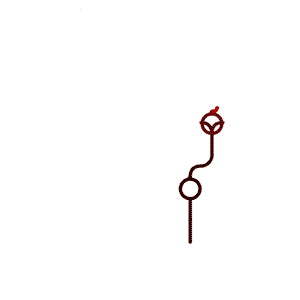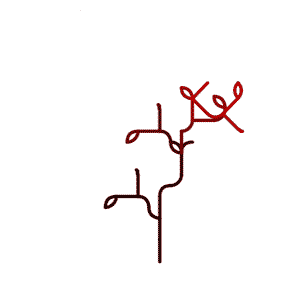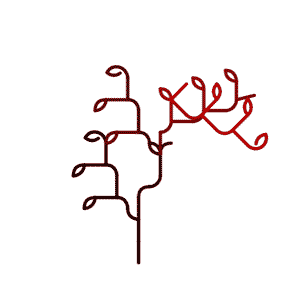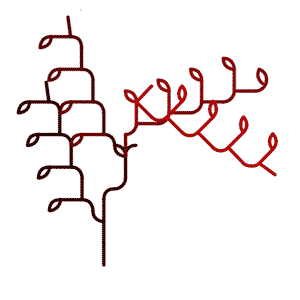
… or by an animation that interpolates between those generations.
When evolving automatically the fitness value guides the selection of trees. Several characteristics have been tested and included in the computation of fitness, like the outputs dimension, ratio, amount of rotations or amount of drawing elements. By adding the length of the string command efficiency of the tree can be encouraged. Though this allows for example to find the easiest solution to reach large dimension while keeping a 1:1 ratio (a straight line at 45 degrees), it fails at evolving forms that can be defined as beautiful or interesting to the eye of the beholder. Finding criteria for defining beauty in form and structure seems to be impossible. Therefore the manual mode of the program and the subjective selection has proven to be the better design solution.
This L-system shows similarities to biological life as it allows the survival of unused genetic material. Replacement rules that are included in the tree gen are copied from generation to generation even though they are not used for generating the string of drawing commands. Crossover and mutation processes can reproduce the functionality of those rules after being forgotten for many evolutionary generations.
The L-Garden program visualizes the interdependency of the simple, the complex and the random in biological and simulated life. While simple rules produce complex results, randomness guides mutation and leads to progress in evolution.
Coverage
- étapes - issue 176, french print magazine
